Using Dice Games to Develop Math Reasoning and Computational Fluency

Rusty Bresser
Dice have been around for a long time. In fact, dice are the oldest gaming implements known to humankind. There are various claims for who actually invented dice. For example, Sophocles said that dice were created by the Greek Palamedes during the Trojan war. Others say that the dice we know of today came from China over 2500 years ago. Whatever their history, using dice in games of chance and skill continue to intrigue us. Below are some pictures of what dice have looked like throughout history.
Dice have been around for a long time. In fact, dice are the oldest gaming implements known to humankind. There are various claims for who actually invented dice. For example, Sophocles said that dice were created by the Greek Palamedes during the Trojan war. Others say that the dice we know of today came from China over 2500 years ago. Whatever their history, using dice in games of chance and skill continue to intrigue us. Below are some pictures of what dice have looked like throughout history.
Kids love rolling dice. Maybe it’s the physical action of shaking some cubes in the hand and tossing them on a tabletop. Perhaps it’s the mystery of which numbers will land face up on the dice after they go bouncing and clattering across a hard surface. It might even be the lure of subitizing (instantly quantifying) the dots on the dice.
For older students, dice games can serve as springboards into explorations about probability. For elementary school students, dice games are great for developing math reasoning skills and computational fluency. Dice games also provide opportunities for teachers to assess student learning and to differentiate instruction in order to meet a variety of student learning needs. Following are three favorites that span grades 1-5.
Pennies or Nickels?
Grades 1 and 2
How to Play
In this game for grades 1 and 2, players take turns rolling a die until each player has rolled three times. On each roll, a player must decide whether to take pennies or nickels (for example, if a two comes up on the die, a player can take two pennies or two nickels). The winner is the player who gets closest to 25 cents at the end of three rolls (the total may go over or under 25 cents). The game may be played in groups of three or four.
Why It’s a Good Game
- Coin Names and Values: First of all, the game gives students practice learning the names and values of coins and adding to find the total value for a collection of coins.
- Strategic Counting: The game helps students improve their methods of counting and adding. For example, some students find the total value of their coins by counting by ones. With help and experience, students can move to more efficient methods such as counting on or skip counting by fives.
- Mental Math: The game can help students improve their mental math skills.
- Math Reasoning: Pennies or Nickels? also helps students develop their math reasoning skills. Students must make decisions based on how close or how far away they are from 25 cents and must evaluate the reasonableness of their decisions while problem solving
- Formative Assessment: Teachers can use the game context to assess their students’ counting and adding skills, and to encourage players to explain their reasoning. As students play the game, I circulate (or observe on Zoom), and ask questions such as:
- “How much money do you have?”
- “Do you want to take pennies or nickels? Explain.”
- “How far away are you from 25 cents? How do you know?”
- “What number on the die are you hoping to roll? Explain.”
- “If you roll a 6, would you take nickels or pennies? Explain.”
Variation: Teachers can differentiate instruction by changing the game to, Pennies, Nickels, or Dimes? The rules stay the same, but players try to get as close to 50 cents as they can.
Playing in Virtual Environments
When playing this game in a virtual environment, we suggest that you play with a small group of students. We also suggest that you spend time modeling how to access the virtual manipulative links, how to use the virtual materials, and how to play the game: Virtual Coins Didax Dice
Dozens of Dice
Grades 2 – 5
How to Play
- Player one rolls 12 dice, estimates the total, finds the total amount, and explains how they figured it out.
- Player two rolls 12 dice, estimates the total, finds the total amount, and explains how they figured it out.
- Players figure out who has a higher total.
- Continue play, repeating steps 1-3.
Why it’s a Good Game
- Simplicity: The game is simple and takes little or no preparation.
- Strategic Number Organization: Students get to choose how they will organize the dice to find a total amount. There are many different strategies students can use.
- Procedural Fluency and Mental Math: Dozens of Dice provides students with many opportunities to develop their fluency with addition, subtraction, and multiplication, and to improve their mental math skills. It also supports the idea of equivalent expressions.
- Differentiation: Teachers can differentiate instruction by changing the number of dice students roll.
- Formative Assessment: Teachers can use the game context to assess students’ computation skills and their problem solving and reasoning skills. As students play, I circulate (or observe on Zoom) and keep the following questions in mind:
- How are students organizing the dice after they roll? Do they randomly start adding the numbers together, or do they group the dice in ways that prompt them to find the total in a more efficient way?
- Are students able to make a reasonable estimate of the total after rolling the dice?
- Do students apply multiplication or skip counting when finding the total?
- How do players figure out who has more and how many more?
- Are students able to explain their reasoning for organizing and then finding the total after rolling the dice?
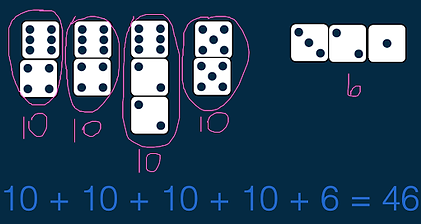
Example Strategy: Make Tens
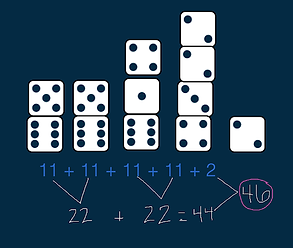
Example Strategy: Make Elevens
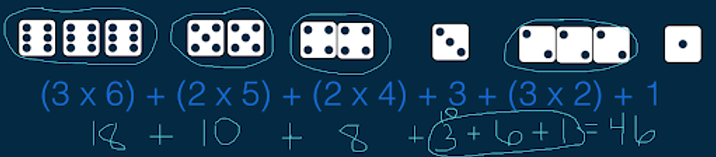
Example Strategy: “Groups of” – Multiplication
Playing in Virtual Environments
We suggest modeling and playing Dozens of Dice in small groups online before having students play with a partner in a breakout room (one student will need to share their screen). Be sure to model how to use the virtual dice roller – Didax Dice.
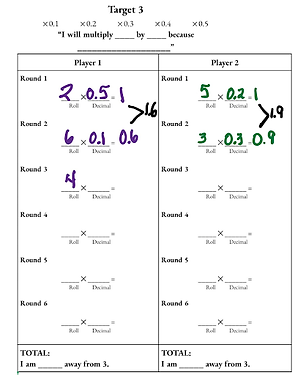
Target 3 (Decimals)
Grades 5 – 8
Object: Get as close to 3 wholes as possible.
Cooperative: How close to 3 wholes can “we” get?
Competitive: Who is closer to 3 wholes?
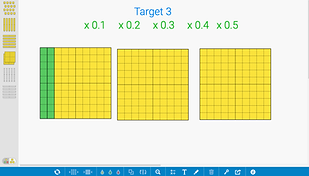
Materials: 1 die, base ten blocks (the flat = 1; the stick = 1/10 or 0.1), recording sheet.
**Virtual Base Ten Blocks**
How to Play
On your turn . . .
- Roll the die and decide if you will multiply the number rolled by 0.1, 0.2, 0.3, 0.4, or 0.5.
- Justify your decision. Example: “I rolled a 6 and I will multiply it by 0.2 because I still have 5 turns to go. 6 groups of two tenths or 6 x 0.2 is 1 and 2 tenths.”
- Cover that amount on your 3 wholes.
Take turns until you have completed 6 rounds. You must use all 6 rounds (6 rolls).
If you played cooperatively, figure out how close to 3 wholes your team got? If you played competitively, who is closest to 3 wholes? How do you know?
Why It’s a Good Game
- Physical Model: Let’s face it, students have a very hard time making sense of operations with decimals. The physical model in Target 3 gives students an opportunity to visualize the value of decimal numbers and scaffolds their ability to make strategic decisions and make sense.
- Strategic Thinking: The requirement of having to use all 6 rolls demands strategic thinking. Some students like to start small, multiplying the roll by 0.1 or 0.2, pacing themselves across 6 rolls. Others like to start big, multiplying the first rolls by the larger decimal numbers and then go small in the end. The fact that players can go over 3 wholes also adds an interesting element to students’ decisions. Strategic thinking is accessible to all students in this game by virtue of the physical manipulatives.
- Lends Itself to Supporting Language Development: All students, especially second language learners, have greater access to justifying math thinking when they have visuals models to talk about. Throughout the game, there are simple ways to support how students structure their talk about the quantities – using “groups of” language is a winning way to think about decimals – “2 groups of five-tenths.” Additionally, a simple sentence frame can support language production. Example: I will multiply ____ by _____ because ___________________. You can provide additional support by keeping a list of the precise vocabulary students use or offering some of the key terms as the need arises.
- Easy to Differentiate: You can differentiate this game by adjusting how many wholes you are trying to cover, how many rounds/rolls make a game, or you could choose to multiply by tenths or hundredths. Another way of varying the game is, instead of isolating each roll into a single turn and decision, roll all 6 rolls at once and then decide what decimal number to multiply each roll by.
- Formative Assessment: By listening to students as they play, you can learn a tremendous amount about their understanding of decimals and decimal operations. How are students choosing and justifying what to decimal to multiply by? Do they recognize what their product will be in relation to whole numbers? For example, if a student rolls a 5, do they realize that multiplying by one-tenth will be less than 1 whole, by two-tenths will be 1 whole, by three-tenths will be more than one whole . . . and by six-tenths will actually be 3 wholes? How are they managing the physical model? How are they reading the decimal numbers? What vocabulary are they using to talk about the math? Is it precise? Do they need more language supports? What are they learning from their mistakes?
Playing in Virtual Environments
Target 3 works well with The Math Learning Center’s “Number Pieces” app. Students can play collaboratively and share their screen on Zoom. If they play competitively, they will each need to have the app opened on their own computer.
Give students a Reason for Using Mathematics
Dice games usually have a purpose for using mathematics. Whether it’s to try to get as close as possible to a target number, earn more points than your opponent, or to find an efficient way to find a total, dice games motivate and engage students because they are enjoyable and give students a reason to use math to solve problems.
Dice games also give our students opportunities to make decisions. Should I take nickels or pennies? And if I choose one or the other, how will that affect how close I will be to the target number? If I multiply the number on the die by x 0.3, what will happen to my score? These types of decisions put students in the driver’s seat as they engage in math reasoning and problem solving for a purpose.
And finally, dice games give teachers many opportunities to formatively assess their students computational skills, and to find ways to differentiate instruction so that all students can play and learn.