Pattern Block Fractions: Adding Fractions with Like and Unlike Denominators

I was recently visiting some friends at their house in the desert, and one of them was making pancakes for breakfast. “Hey, I’m looking at two recipes,” he called out from the kitchen. “One calls for doubling 2/3 cup of mix and the other says to double 3/4 cup. Which will make more pancakes?” I love it when math works its way into breakfast time. 

Like a good teacher, I didn’t tell him the answer but asked, “What do you think?,” which prompted an animated discussion.  Before you read on, think about the problem. Try to solve it in your head, and notice where your thoughts lead you. 

So, What’s the Answer?

A week later, I was walking with another friend, and I was curious how he would think about the problem (asking your friends to indulge you about math can be risky).

“Which is greater, 3/4 or 2/3?” I asked. He paused, and then said, “I think they’re about the same size.” 

“Why do you think that?” I probed. 

“Wait! Maybe 3/4 is greater.”

“What made you change your mind?” 

“I’m thinking of the quiche you make in those round pie tins. I’m visualizing 3/4 of a quiche and 2/3 of a quiche. Three-fourths is the one that I’d rather have because it looks bigger. Also, 3/4 is only a fourth away from a whole, and 2/3 is 1/3 away. Three-fourths is closer to one whole, so it’s greater.”

I appreciated that he had two different ways to think about the problem. “So, you’re convinced that 3/4 is greater than 2/3?”

 He nodded. 

“Is 3/4 a little or a lot bigger?” I asked. 

“Just a little,” he said. 

We walked a bit further, and then I asked him how much bigger 3/4 is than 2/3.” 

“It’s a teeny bit bigger,” he joked. 

I wouldn’t let him off the hook and asked again, “Exactly how much bigger?” He was stumped. 

“Well, what if you had to find out how much bigger 3/4 is than 1/4? What would you do?”

He immediately figured out the answer. I asked him why that problem was easier, and he said that all the pieces (fourths) were the same size. And this led to his epiphany: when we add or subtract fractions that have unlike denominators, one way to solve is make the denominators (the size of the pieces of the whole) the same size (in this case, the size of part of a quiche). 

A Fraction Lesson Using Pattern Blocks

Visualizing parts of a whole using a round pie tin of quiche helped my friend make sense of fractions. And, his thinking reminded me how valuable visual models are in helping learners understand part-to-whole fractional relationships, especially when combining and separating numbers that are smaller than one.  

In the next part of this post, you’ll read about a fraction lesson that my colleague, Karyn Conner, and I developed using Pattern Blocks. The lesson not only serves to help students learn about part-to-whole relationships, but it also can help them begin to wrap their brains around the epiphany my friend had about adding and subtracting fractions with unlike denominators. 

Directions:

Materials: A collection of Pattern Blocks for a small group (leave out the orange squares and tan parallelograms), paper, and pencil. 

Step 1: Explore the Pattern Blocks. Distribute Pattern Blocks, and ask students what they notice and wonder. 

Step 2: Find Fractional Relationships. After students share what they notice and wonder, ask them to explain what the fractional value of each block is if the yellow hexagon is equivalent to one whole. When they are finished, record the values of each block on chart paper. 

Provide the following cause and effect sentence frame to support students as they talk about the blocks: If ______, then _______. For example, they might say, “If the hexagon is equivalent to one whole, then the triangle is equivalent to one-sixth because six triangles make a hexagon, and one of them is one out of six.”

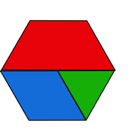
Step 3: Find the Value of Different Shapes. Display a simple shape made from a few blocks. Ask the class what the total value of the shape is, knowing the fractional value of each block. For example, the shape below has a value of one-half: 1/6 + 1/3 = 1/2 or, another way of thinking about it, is 1/6 + 2/6 = 3/6.

Students may notice that you can substitute the blue block for two green blocks (or 1/3 for 2/6) so that all the pieces are one color (have the same denominator or same-size pieces).  This makes life a lot easier. 

Show another example (see below), and have students think of different equations that would equal one whole. For example: 1/2 + 1/6 + 1/3 = 1, or 3/6 + 2/6 + 1/6 = 1 (or 6/6). If they need help, consider asking them if they can find a way to make all the shapes the same color. 

Show yet another example (see below), this time display a shape that’s more complicated and have students work with a partner to determine the total value of the shape. Work with the class to explore different equations that would represent the shape’s total value. Emphasize that making the shapes have the same color (or denominator) can make it easier to add them together. For example, adding 3/6 and 1/2 (the three green triangles and the red trapezoid) can be challenging. But seeing the problem as 3/6 plus 3/6 (make the red trapezoid equivalent to 3 green triangles) makes it much easier to add the pieces together. 

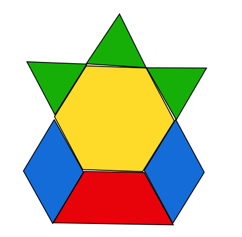
While fourth graders are expected to add and subtract fractions with the same denominator, fifth graders must find sums and differences of fractions that have unlike denominators. The Pattern Block fractions lesson is appropriate for both grades. 

Step 3: Create Pattern Block Shapes. Direct students to create their own shapes and determine the total value of the shape. We suggest putting a limit on the number of blocks students use for their shapes. For example, have students make a shape with between 4 and 8 blocks, at least two different colors. 

Step 4: Gallery Walk. Consider having the class engage in a gallery walk, circulating the room observing and figuring the different students’ shapes and their values. 

Step 5: Record and Explain on Paper. After the gallery walk, have students return to their seats, trace their shape onto paper, and write equations that represent the shape’s value. Encourage them to explain their thinking in writing. 

In the Classroom with Fifth Graders 

When I visited Kathy Seckington’s fifth grade class, they were just about to begin a unit on operating on fractions. As Kathy made her way through the first parts of the lesson, I was impressed by how engaged and motivated her students were. 

Being able to visualize wholes, halves, thirds, and sixths with concrete materials provided access for everyone. For example, during the first part of the lesson as students explored, they immediately identified fractional relationships between the blocks. I heard comments like, “You can make a hexagon with six triangles!” and “Three blue quadrilaterals make one hexagon!” Others began to use fractional language, making claims such as, “The triangles are worth one-sixth!” or “Two triangles make one rhombus so two sixths are the same as one-third!”

Examining Student Work Samples

When they were ready to build their own shape with the blocks, students had a lot to report. They loved being able to make their own shapes. Following are just a few examples from a stack of impressive work. 

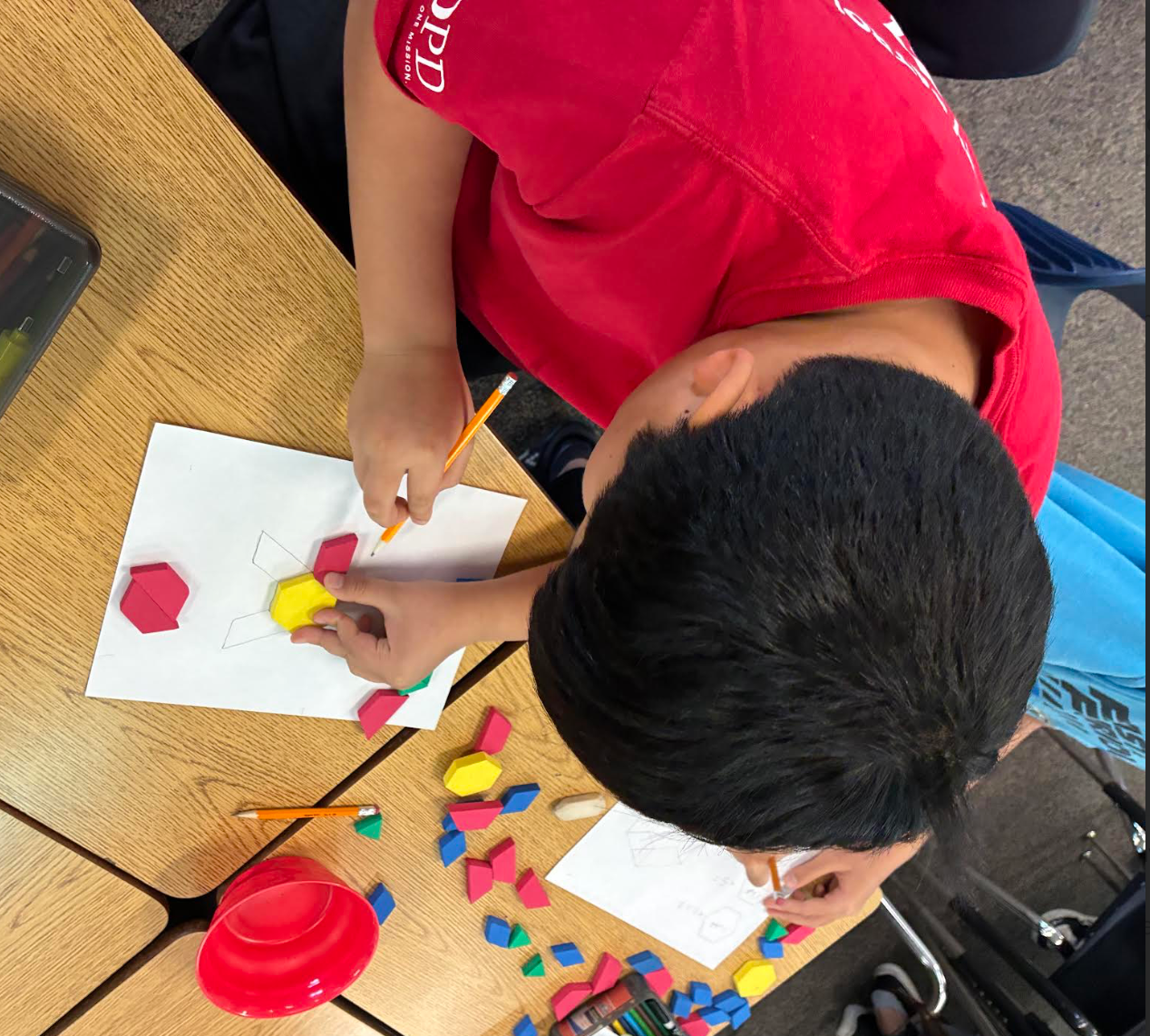
This student notes that, “In fraction addition, you must make all the denominators the same. That is why I made all the shapes’ denominators 6.” She was able to trade wholes, halves, and thirds for sixths to make the addition easier. 

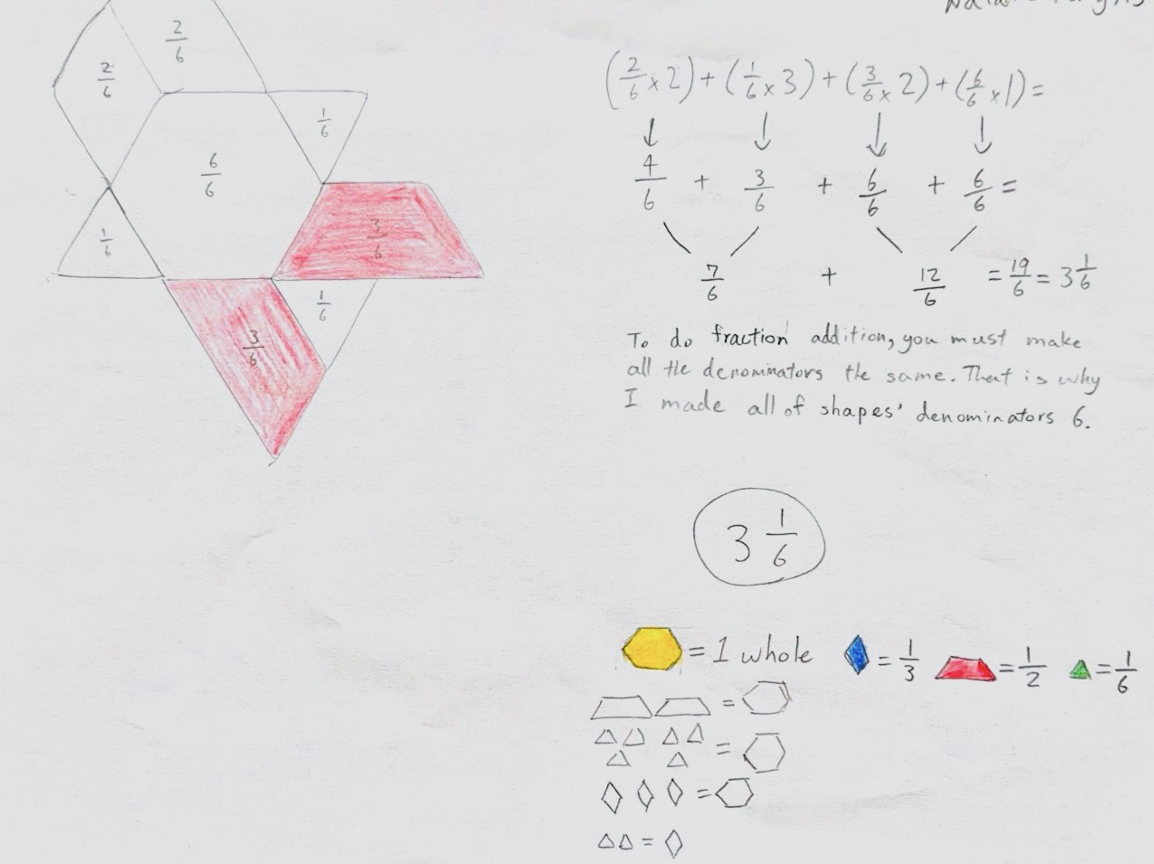
This student clearly shows how they converted halves and thirds to sixths, noting equivalent fractions, and cleverly incorporating multiplication in their explanation. 

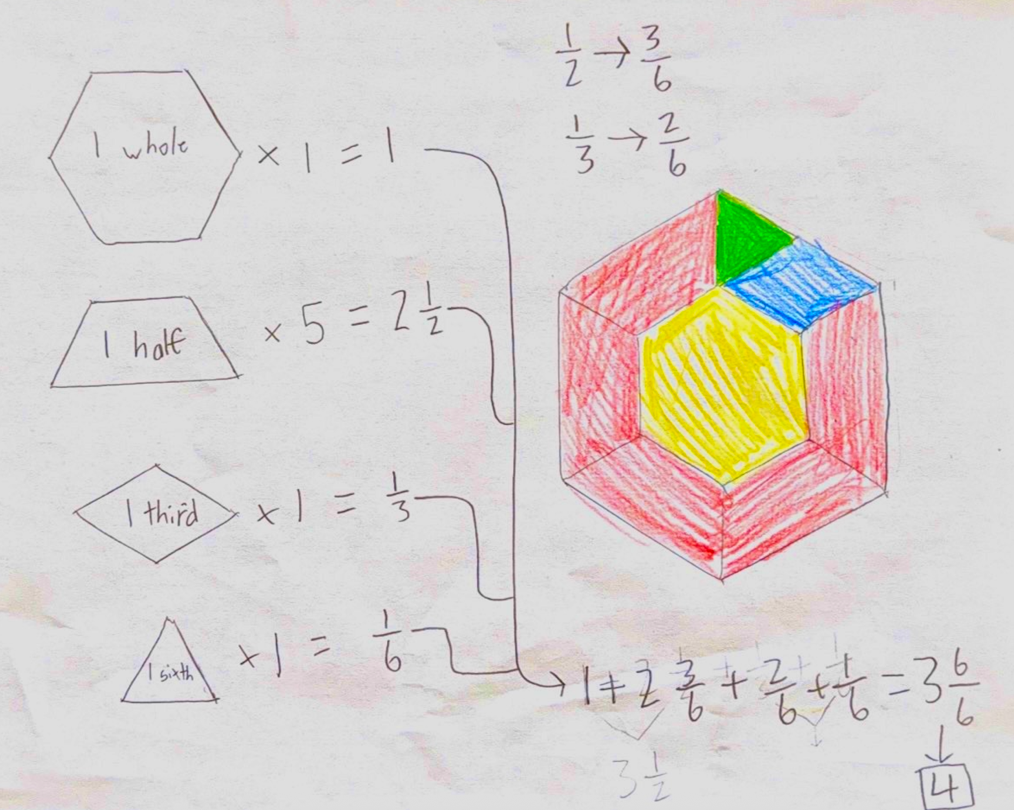
This student got creative and made a Christmas tree from her blocks. Her equations clearly show her understanding of equivalent fractions.

And finally, this student’s work is a fine example of clearly showing how they combined the fractions to arrive at 3 2/3. 

The Hallmarks of a Good Math Lesson

I loved watching Kathy teach this lesson, and I was so impressed by the students and their work. Teachers need well-crafted math lessons to work with. And students deserve to have lessons that are interesting and engaging, include opportunities for differentiation, and provide just the right amount of scaffolding and visual support to bring meaning to abstract ideas, just as pancakes and quiche helped my friends make sense of fractions. 

Most importantly, good math lessons allow for student agency. That is, they afford students opportunities to create, to choose, and to take ownership of their own learning. I think the Pattern Block Fraction lesson does all of this and more. We hope you try it out!